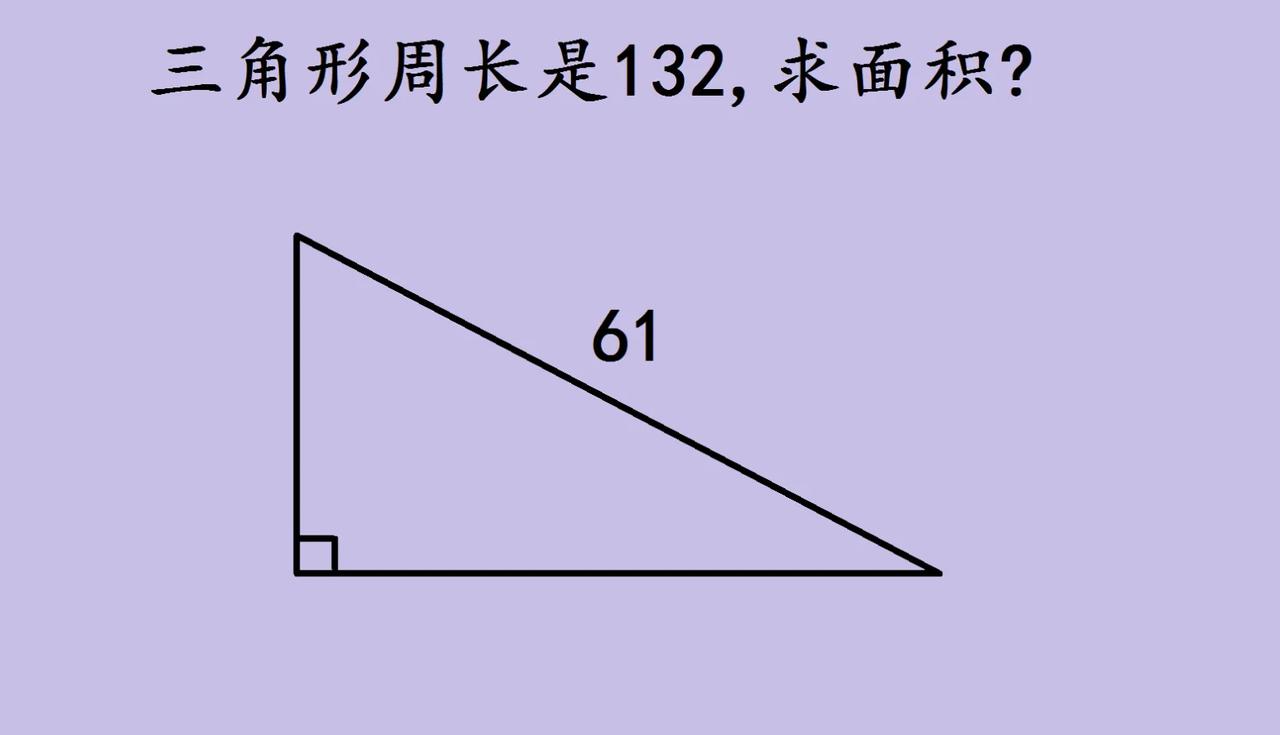
巧解直角三角形面积，周长来帮忙 今天遇到个有意思的直角三角形问题，已知周长132，斜边61，求面积。 首先，直角三角形面积是两直角边乘积的一半，所以关键得找两直角边。设它们为a、b，斜边c = 61 。因为周长132，所以a + b + c = 132，就能算出a + b的值啦。 又因为直角三角形满足勾股定理，a² + b² = c² 。这时候可以想想，(a + b)² 展开是a² + 2ab + b² ，那ab就等于[(a + b)² - (a² + b²)]÷2 。把前面得到的a + b和c代入，就能算出ab，进而求出面积。 这种利用周长、勾股定理结合的思路，把看似无关的条件串联，巧妙找到解题钥匙，数学就是这样，好多问题换个角度、结合不同知识，就能迎刃而解，探索过程超有趣，大家也可以试试这种思维方法呀～
