[LG]《Topological Invariance and Breakdown in Learning》Y Yang, T Poggio, I Chuang, L Ziyin [University of Michigan & MIT] (2025)
《Topological Invariance and Breakdown in Learning》解读
🔍 本文揭示:在广泛的置换等变学习规则(如SGD、Adam)下,训练过程会诱导神经元间的双Lipschitz映射,强烈约束神经元分布的拓扑结构。
⚖️ 关键发现:
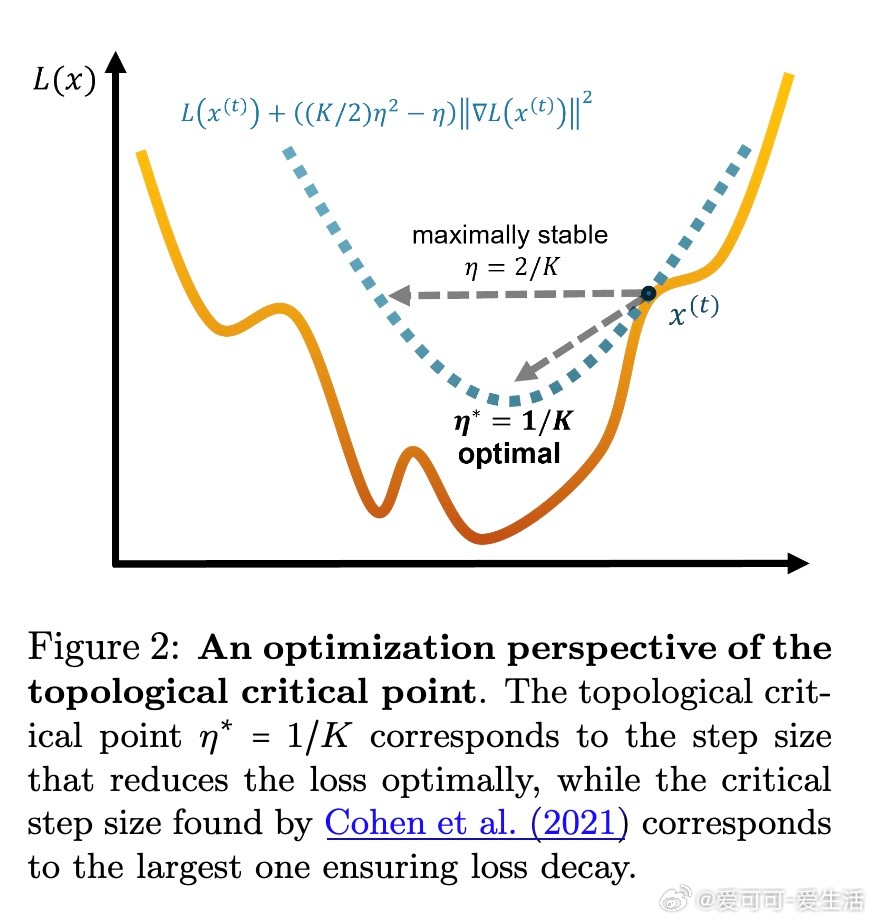
1️⃣ 学习率 η 有一个临界点 η*:
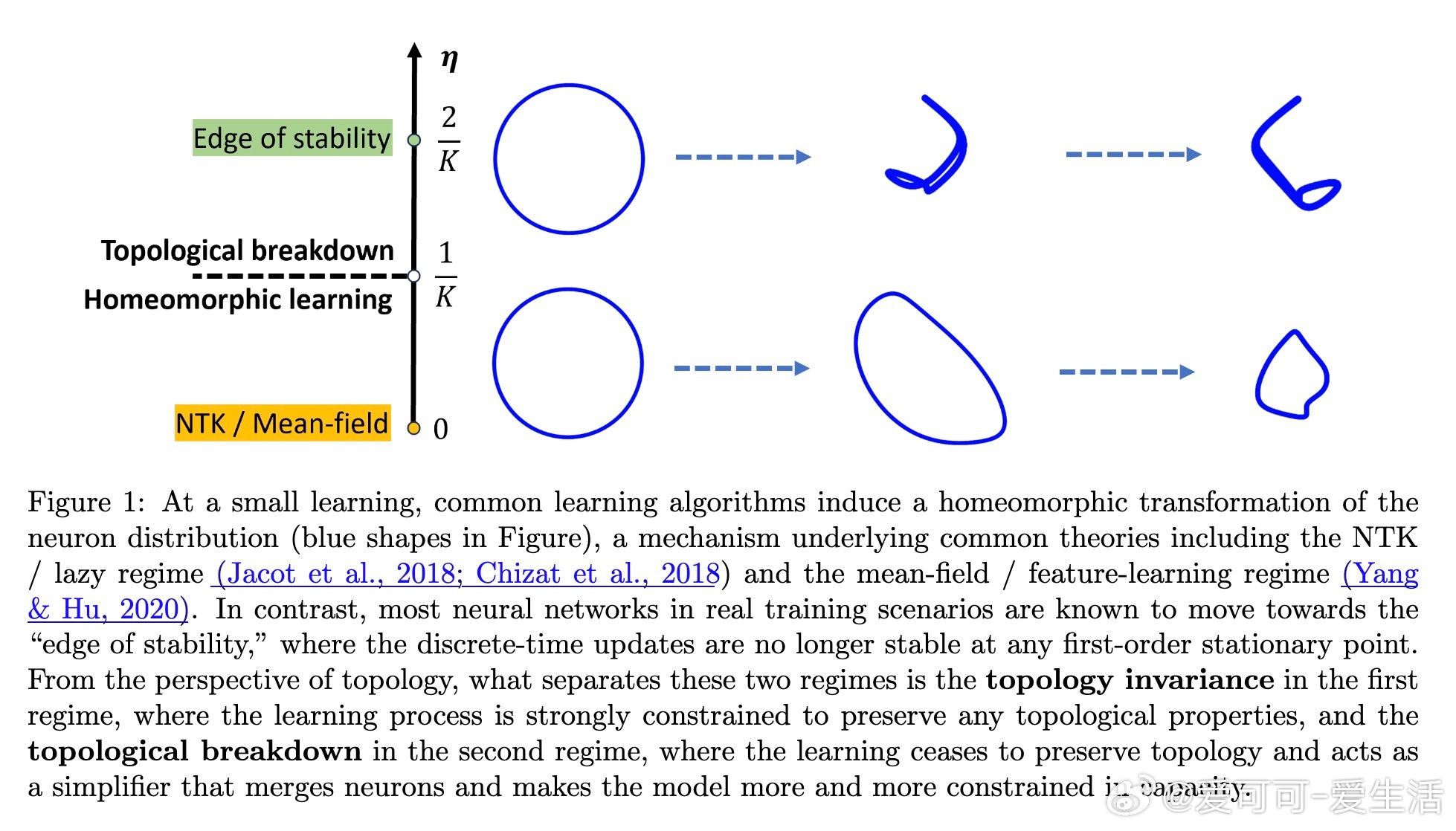
- 当 η < η*,训练保持神经元拓扑不变(拓扑不变性),模型表现为平滑优化阶段,拓扑结构稳定。
- 当 η > η*,拓扑不变性破裂,训练允许拓扑简化,神经元流形逐渐粗化,模型表达能力降低,这是拓扑相变现象。
2️⃣ 该理论不依赖具体架构或损失函数,具有普适性,适用于深度学习的拓扑研究。
🌐 理论意义:
- 置换等变性导致学习动态产生拓扑约束,低学习率阶段对应拓扑保守的优化,符合NTK和mean-field理论;高学习率阶段对应拓扑简化,与“边缘稳定”现象相呼应。
- 拓扑简化意味着参数对称性恢复,模型参数有效数目下降,影响模型容量与泛化。
🧪 实验验证:
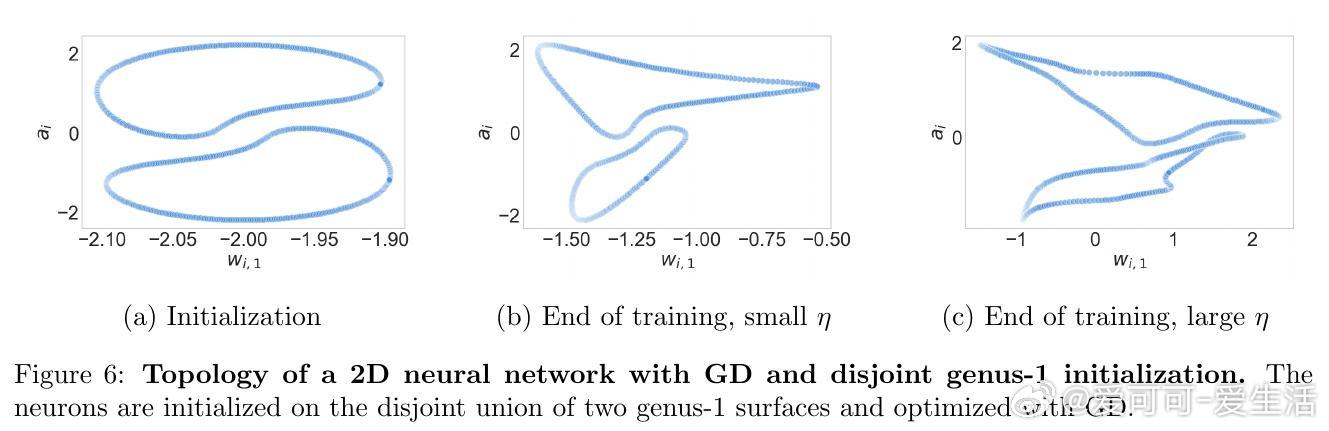
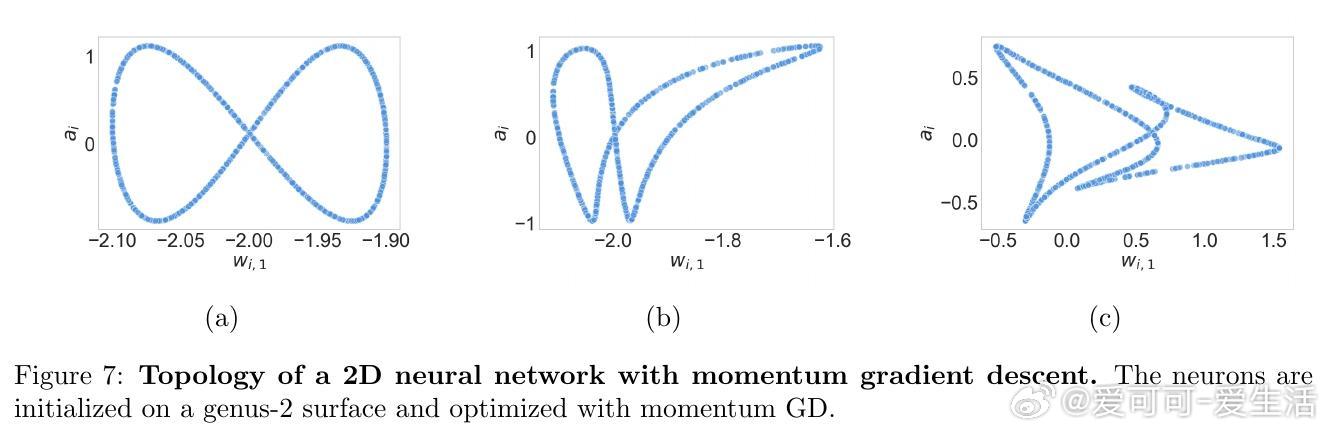
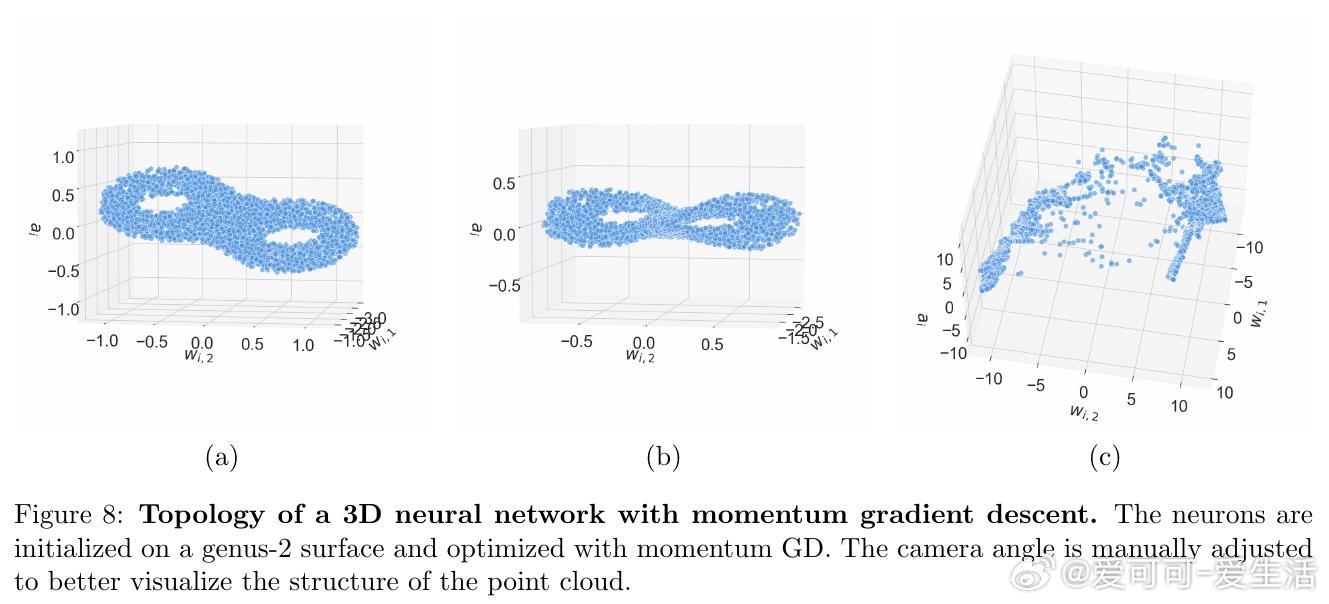
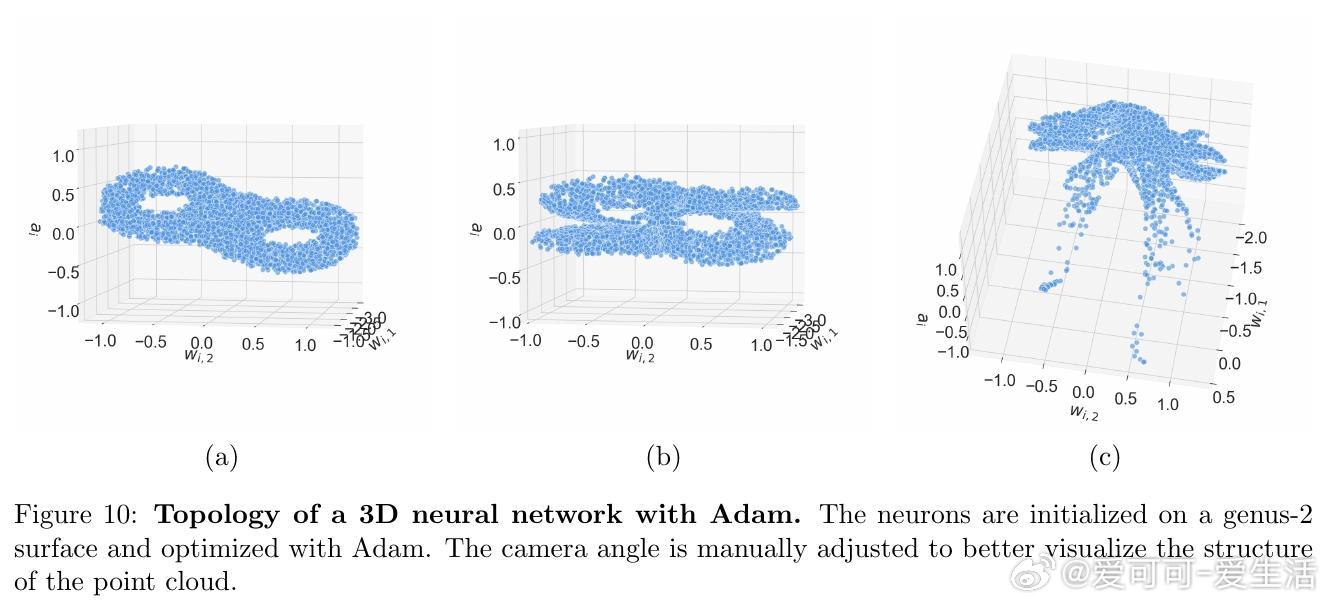
- 低维网络视觉化神经元拓扑:小学习率保持初始拓扑,大学习率引发拓扑变化。
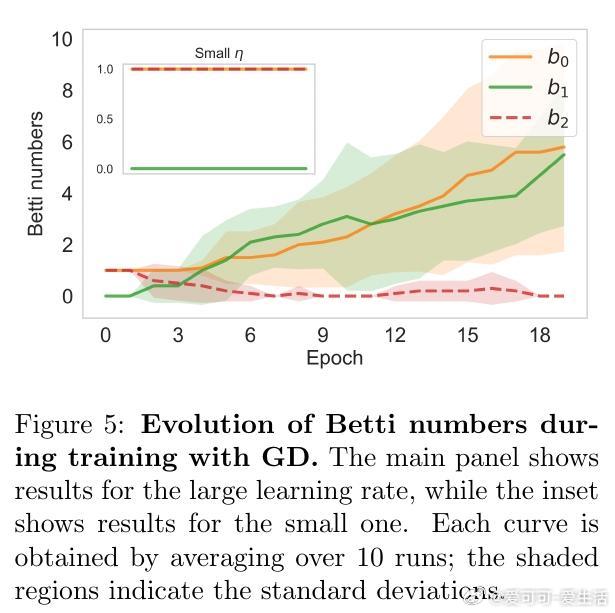
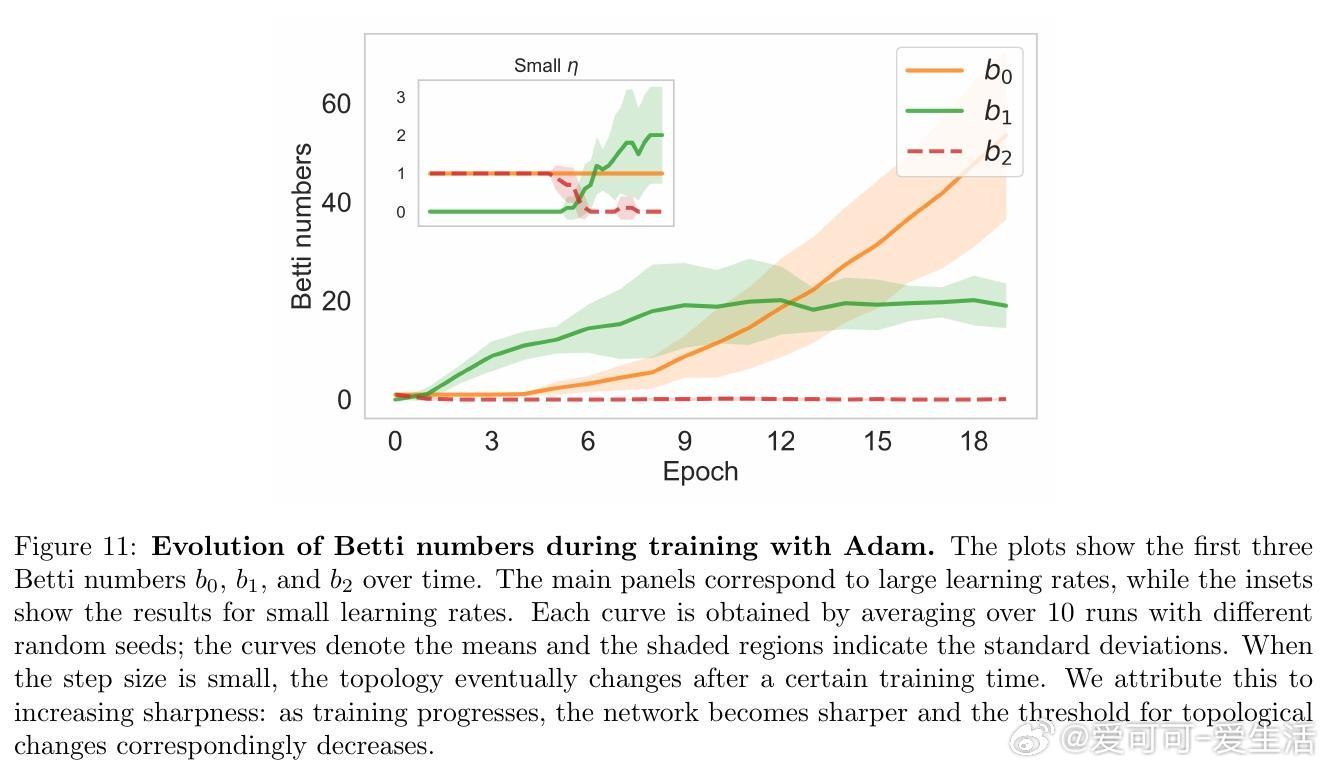
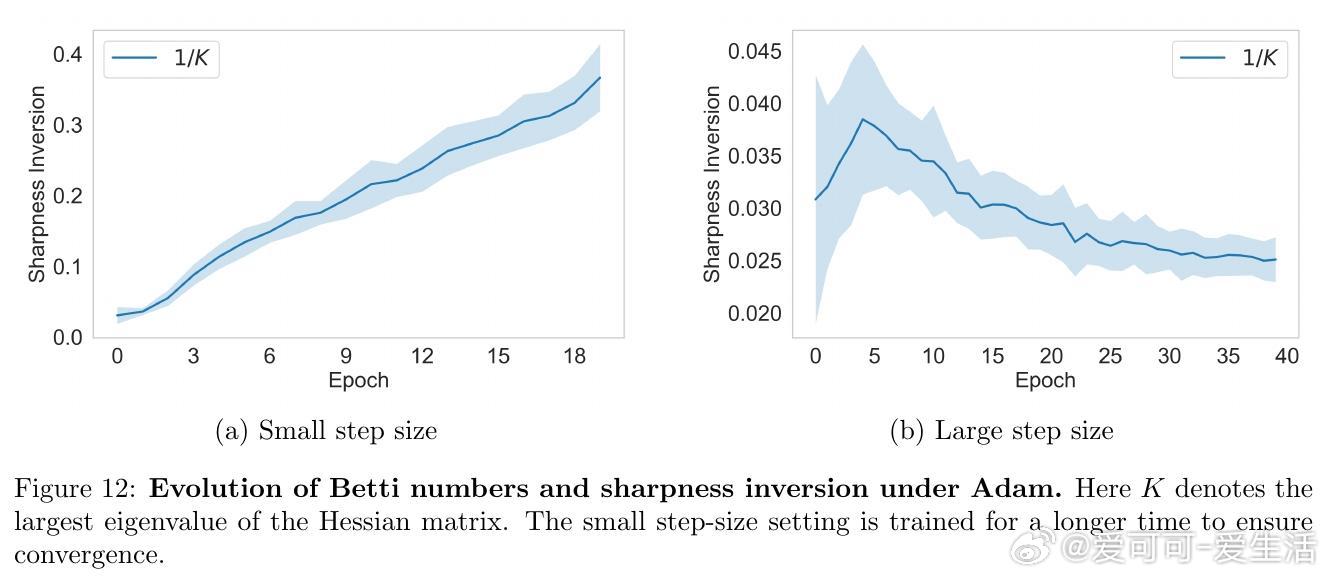
- MNIST任务中测量Betti数(拓扑不变量)验证理论,支持拓扑临界点存在。
- 不同优化器(GD, Adam, Momentum)均符合理论预测。
💡 应用展望:
- 该拓扑视角或助于设计更有效的学习率调度策略(如先大后小),平衡探索与稳定。
- 深度学习理论需考虑拓扑相变,现有NTK等理论仅适用于小学习率阶段。
- 拓扑方法为理解训练动力学提供新工具,连接数学拓扑与物理相变理论。
👉 详细理论及证明见论文全文,附实验与代码验证。
原文链接:arxiv.org/abs/2510.02670
深度学习 拓扑学 优化理论 神经网络 机器学习理论